Cassini States

Overview

Demonstration of a planet’s obliquity evolution under the influence of tides and gravitational perturbations from another planet, resulting in capture into a “Cassini state.”

Date

07/25/18

Author

Russell Deitrick

Modules

EqTide DistOrb DistRot

Approx. runtime

54 seconds

A damped orbital-rotational system can enter a “Cassini state,” in which a planet’s rotational axis, orbital axis, and the local total angular momentum vector are all coplanar. In this case, we consider a system in which tides from the star damp the rotation rate, obliquity, semi-major axis, and orbital eccentricity. Tides tend to damp the rotational axis so that it is perpendicular to the orbital plane, but perturbations from other planets drive the obliquity to higher values. Over time, the systems settles into a damped-drived state in which the obliquity is non-zero, but also not oscillating. This example is modeled after Winn & Holman (2005), see their Fig. 2.

To run this example

vplanet vpl.in
python makeplot.py <pdf | png>

Expected output

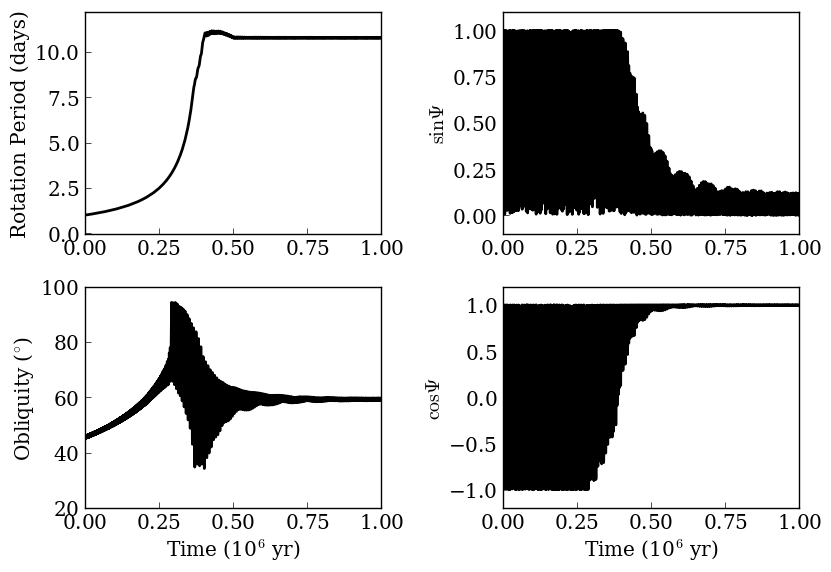
examples/CassiniStatesEvol.png

An Earth-mass planet damping into Cassini state 2 under the influence of tides and perturbations from an 18 Earth-mass companion planet. The bottom right panel shows a “Cassini parameter” which is locked at either 1 or -1 indicates the presence of a Cassini state. At the end of the simtulation, the inner planet is synchronously rotating, but its obliquity is approximately fixed at 60 degrees. This example is constructed to be similar to Figure 2 of Winn & Holman (2005).

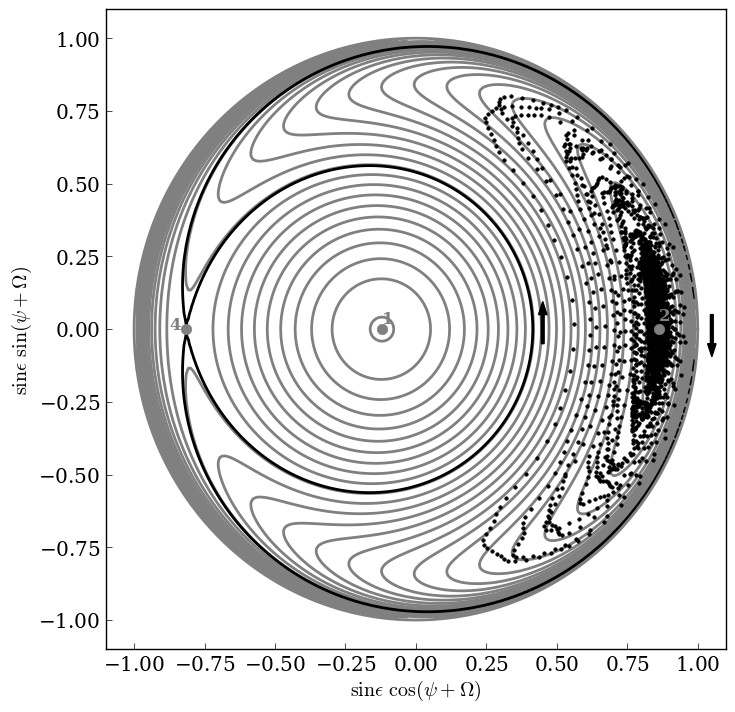
examples/CassiniStatesSection.png

Phase space of the three prograde Cassini states (numbered). The gray curves show lines of constant Hamiltonian (Equation 5 in Winn & Holman [2005]) and the black curve shows the separatrix between states 1 and 2. The three possible Cassini states for this system are denoted by the light gray numbers 1, 2, and 4. This case is constructed to be similar to the illustrative case shown in Figure 2 of Winn & Holman (2005), with -g/alpha ~ 0.75 and i = 6 deg. The location of the planet’s pole after ~400 kyr is shown as the black points, with the arrows depicting the direction of evolution. As the planet’s spin is damped by tidal torques, its obliquity sinks into Cassini state 2.