Chaotic Eccentricity-Inclination Resonances
Overview
Planets in a mean motion resonance and in which the orbital planes are inclined relative to each other can evolve chaotically, but still survive for over 10 Gyr. This example reproduce System U in Barnes et al (2015), see their Fig. 13.
An animation of this system is available here.
Date |
12/20/18 |
Author |
Rory Barnes |
Modules |
SpiNBody |
Approx. runtime |
14 hr |
To run this example
vplanet vpl.in
python makeplot.py <pdf | png>
Expected output
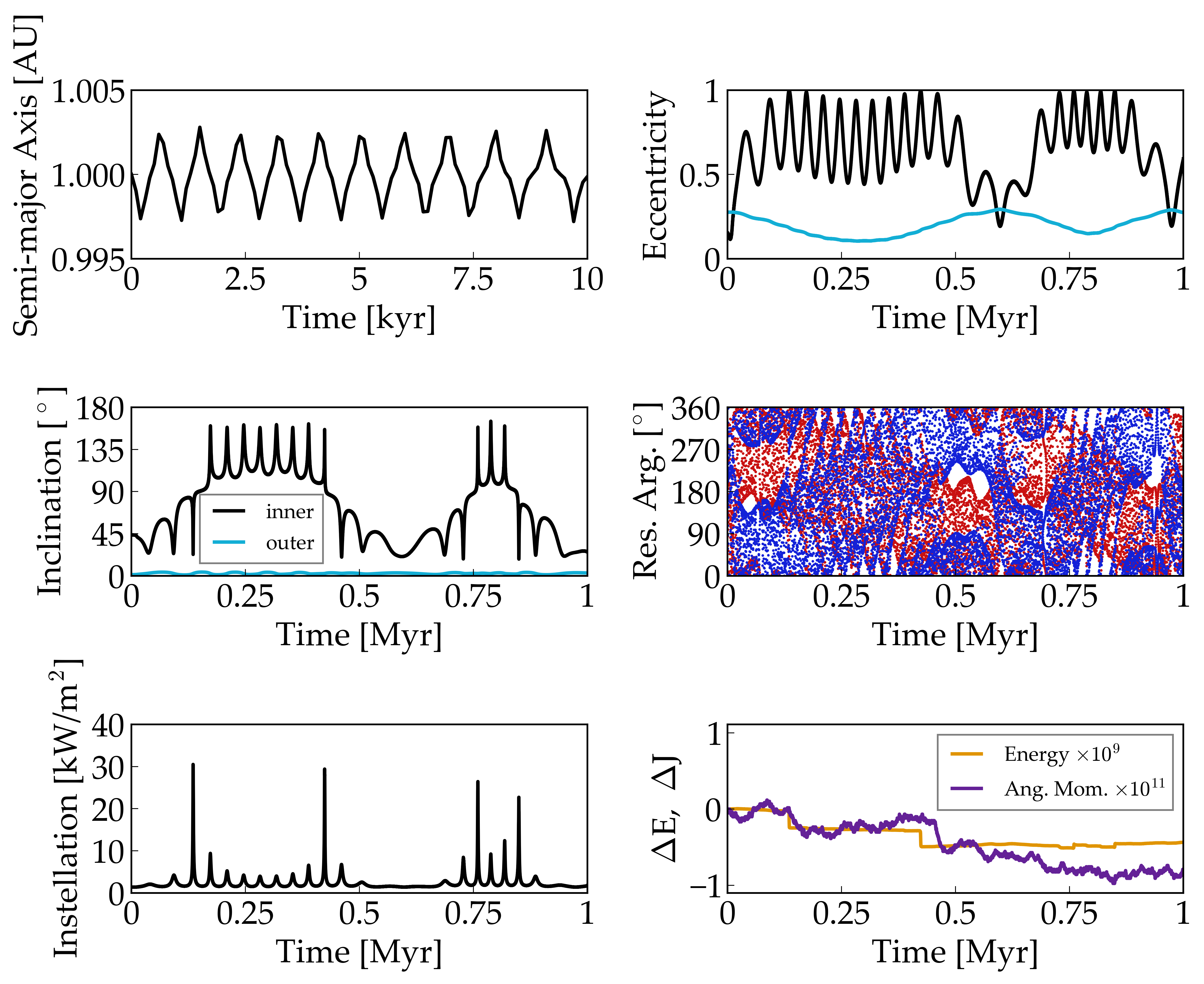
Top Left: The semi-major axis evolution of the inner (Earth-like) planet changes by about 0.5% every 1000 years. (Note the x-axis scale is different for this panel.) Top Right: The eccentricity evolution of both planets, inner in black, outer in blue. The inner planet’s eccentricity exceeds 0.99 in several instances. Middle Left: The inner planet’s inclination can grow larger than 160 deg. Middle Right: The two eccentricity-resonance arguments show complicated behavior, with high amplitude libration on short timescales, but circulation on longer timescales. Bottom Right: Intellation of the inner planet. Although typically around the Earth’s solar constant of 1366 W/m^2, increases over a factor of 30 are possible during epochs of star-grazingly-high eccentricity. Bottom Right: Energy (orange) and angular momentum (purple) are conserved to high precision in this run. The slow drifts are typical of the 4th order Runge-Kutta scheme in vplanet. Note that Barnes et al (2015) found this system to be stable for 10 Gyr.